I Have A Math Minor
And really good spacial awareness. But you know what I cannot (ever) reliably do? Geometry. I can't calculate most geometric things without significant difficulty, tears, or...uh...errors.
Before we get into that, look at all the beautiful yellow and gold fat quarters I got from Joanns! There are thirty of them, to add to the thirty I already had, and the other scraps I'm planning to use on this project. (I know they don't look like thirty...there are doubles of the entire left column and the top two in the center, triples of the lower three in the center, and the right column are singles.) That's about 15 yards of fabric, just so we're all clear.
On top of the vast quantities of fabric I've collected for this project, I've been very carefully saving the partial hexis from the edges of my fat quarters, and pinning them to piece together into yet more hexagons. I'm starting with making eight more hexagons of each fabric print, to bring the total number of hexagons of each print up to 144 (YES, A WHOLE GROSS. OF EVERY PRINT. IT'S DELIGHTFUL). That leaves me with enough halfsies for another eight hexis, but I'm stashing those leftovers until I have all my pieces cut, and then I'll make hexis that are half-and-half from them.
I'm still not emotionally prepared to tell you how tremendously I screwed up the math for this quilt, so instead we're just gonna look at this soothing and extremely satisfying hexagon for a bit.
Yeah...let's just keep looking at it. Isn't it lovely?
HOKAY, so: the math. The math for the quilt. The quilting math.
I had a truly incomprehensible geometry failure when I was doing my initial calculations for this quilt, which I wanted to make 8x6 feet. Large, but not unbelievably so. I'm using regular hexagons with a 1-inch edge. In my fevered brain, this meant that each hexagon must occupy a 1x1-inch space, so I'd need 96 of them along the long edge, and 72 on the short edge, which equals 6912 hexis—plus halfsies to fill the crenellated edges and make the quilt actually rectangular, because even I'm not interested in binding a rippling hexagony edge. (Oh, oops, I shouldn't have imagined that. Maybe I am interested...)
Spoiler alert: hexagons with 1-inch edges don't occupy 1-inch squares. They just don't.
In fact, they're 1.73 inches flat side to flat side, and 2 inches point to point. That's...that's very different. Using my original hexagon numbers, 96 on one side and 72 on the other, I could have a 10x16-foot quilt, or a 12x13.8-foot quilt (it depends on the orientation of the hexis). I was informed that I Could Not Do That because it would never ever ever be able to be washed.
I still had to think about it.
And another friend commented that if I made a 10x16-foot quilt, it could then be both a tent and a quilt at the same time. Which was a tempting idea: enveloped in warmth and yellow, to ward off the semi-eternal winter we've been having.
But then I was reminded that even an industrial washing machine would struggle with a 10x16-foot quilt, no matter how gorgeous it was (in fact the gorgeousness would probably be a detriment, given how often washing machines eat my favorite socks). So I resigned myself to creating (two) smaller quilt(s) with the fabric I'd already acquired: 60 fat quarters at 144 hexis per pair equals 4320 hexis total. If I use 3360 of these to make an 8x10-foot quilt (yes, really), I'll have 960 remaining, which I can arrange into a 4x5.6-foot "lap" quilt. Perfectly reasonable.
A day went by, and I suddenly had a terrible thought. I'd corrected the dimensions of the hexis...but they're still hexagons, not rectangles. Hexagons tile by partially overlapping in both directions. The total area they'd cover wasn't described by [number of hexis multiplied by flat-to-flat width]x[number of hexis multiplied by point-to-point width], but by...uh...something rather more complex.
Thank god high schoolers have to work this problem a lot, and math people have taken pity on them and posted the answer all over the joint. Rather than use dimensions of individual pieces at all, the way to find a hexagonal tiling of a given rectangular space is to find the total area of the space (say 80 square feet, just for a randomly selected example) and divide it by the total area of the tiles you're using (2.6 square inches, for a regular 1-inch edge hexagon). YAY! So now the bigger quilt's dimensions are 8x9.4 feet, still using 3360 hexis, and the smaller is 4x5.4 feet, using the remaining 960 hexis—because the number of hexis possible with my collected fat quarters has remained static, if slightly underestimated.
Nota bene: The area measurement in my scribbles up top is wrong. You can find the area of a hexagon using only the width multiplied by the average of the side length and the height...but you have to actually use the right measurements, instead of swapping out the side length for the shorter of the two widths.
...yes, that does mean I'm now making my third set of corrections to the initial calculations. Right now. As I write this post. I am gonna be so good at hexagonal math by the end of this project, because I will have made all the possible mistakes already.
Let's take another wee break, shall we? So far I've been stacking finished hexagons on top of the bookshelf with my spindles and The Porg, because they're very pretty, and it makes keeping count much easier. I've added two more prints since I took this photo, though, and it's getting a little crowded, so I'll need to come up with a new system soon. Because it's important to have projects that support your projects.
Okay, time to finish the math (maybe) [hopefully] {dear lord, let it end}. So I want to make an 80-square-foot quilt, which is 11,520 square inches. Divided by the correct area-of-a-1-inch-edge hexagon (2.598 square inches), I'll need about 4,435 hexagons for the large quilt. The smaller quilt has an area of 3,226 square inches, which divided gives about 1,242 hexagons.
To stick with those quilt dimensions, I'd need about 5,677 hexagons, which means I'm 1,357 hexagons short, if I count only the fat quarters I've already acquired. That sounds like a lot, but I'd only need 18.84 fat quarters to make up the difference (or about 4.75 yards of fabric, assuming 45-inch width). And my hexi calculations have never included the irregular stash remnants I'm planning to add for textural variation:
• .81 yards plain yellow cotton
• 1 yard plain gold silk
• .94 yards plain blue silk
• .44 yards plain cream silk
• .59 yards plain brown silk
• 1.75 yards printed mustard cotton
• .5 yards printed light yellow cotton
That's almost exactly 6 yards of fabric.
I might still get just a few more prints...because it wouldn't do to have too many hexis of the same pattern, and I'm not sure I want to eke every possible hexagon out of the silks. They're meant to be textural accents, which implies that they shouldn't occur at the same (or greater) frequency as most of the cotton prints. If I only used half a yard of the mustard print, and assumed no more than .25 yard of each silk, I'd be adding 2.81 yards of fabric to my existing fat quarters, which would leave me about 2 yards short.
(I can stop whenever—shut up, stop laughing—whenever I want.)
 |
| So bright and cheerful. Unlike this neverending winter. |
 |
| Those pieces with the white selvedge make me a little nervous, but we'll see what happens. |
 |
| Still in love with the hexis where a motif ends up perfectly framed. |
Yeah...let's just keep looking at it. Isn't it lovely?
 |
| Translation: screaming. |
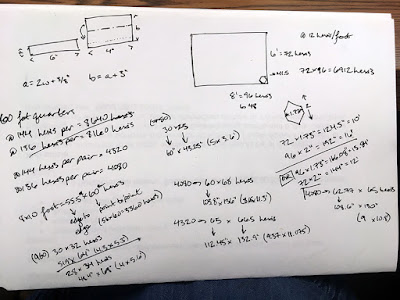
I had a truly incomprehensible geometry failure when I was doing my initial calculations for this quilt, which I wanted to make 8x6 feet. Large, but not unbelievably so. I'm using regular hexagons with a 1-inch edge. In my fevered brain, this meant that each hexagon must occupy a 1x1-inch space, so I'd need 96 of them along the long edge, and 72 on the short edge, which equals 6912 hexis—plus halfsies to fill the crenellated edges and make the quilt actually rectangular, because even I'm not interested in binding a rippling hexagony edge. (Oh, oops, I shouldn't have imagined that. Maybe I am interested...)
Spoiler alert: hexagons with 1-inch edges don't occupy 1-inch squares. They just don't.
In fact, they're 1.73 inches flat side to flat side, and 2 inches point to point. That's...that's very different. Using my original hexagon numbers, 96 on one side and 72 on the other, I could have a 10x16-foot quilt, or a 12x13.8-foot quilt (it depends on the orientation of the hexis). I was informed that I Could Not Do That because it would never ever ever be able to be washed.
I still had to think about it.
And another friend commented that if I made a 10x16-foot quilt, it could then be both a tent and a quilt at the same time. Which was a tempting idea: enveloped in warmth and yellow, to ward off the semi-eternal winter we've been having.
But then I was reminded that even an industrial washing machine would struggle with a 10x16-foot quilt, no matter how gorgeous it was (in fact the gorgeousness would probably be a detriment, given how often washing machines eat my favorite socks). So I resigned myself to creating (two) smaller quilt(s) with the fabric I'd already acquired: 60 fat quarters at 144 hexis per pair equals 4320 hexis total. If I use 3360 of these to make an 8x10-foot quilt (yes, really), I'll have 960 remaining, which I can arrange into a 4x5.6-foot "lap" quilt. Perfectly reasonable.
 |
| I was also using this to draw a diagram of a pocket, and to figure out the color sequence for my blanket. |
Thank god high schoolers have to work this problem a lot, and math people have taken pity on them and posted the answer all over the joint. Rather than use dimensions of individual pieces at all, the way to find a hexagonal tiling of a given rectangular space is to find the total area of the space (say 80 square feet, just for a randomly selected example) and divide it by the total area of the tiles you're using (2.6 square inches, for a regular 1-inch edge hexagon). YAY! So now the bigger quilt's dimensions are 8x9.4 feet, still using 3360 hexis, and the smaller is 4x5.4 feet, using the remaining 960 hexis—because the number of hexis possible with my collected fat quarters has remained static, if slightly underestimated.
Nota bene: The area measurement in my scribbles up top is wrong. You can find the area of a hexagon using only the width multiplied by the average of the side length and the height...but you have to actually use the right measurements, instead of swapping out the side length for the shorter of the two widths.
...yes, that does mean I'm now making my third set of corrections to the initial calculations. Right now. As I write this post. I am gonna be so good at hexagonal math by the end of this project, because I will have made all the possible mistakes already.
 |
| K calls this piece Porg Builds a Wall. I was thinking more Porg Visits the Giant's Causeway, but sure. |
Okay, time to finish the math (maybe) [hopefully] {dear lord, let it end}. So I want to make an 80-square-foot quilt, which is 11,520 square inches. Divided by the correct area-of-a-1-inch-edge hexagon (2.598 square inches), I'll need about 4,435 hexagons for the large quilt. The smaller quilt has an area of 3,226 square inches, which divided gives about 1,242 hexagons.
To stick with those quilt dimensions, I'd need about 5,677 hexagons, which means I'm 1,357 hexagons short, if I count only the fat quarters I've already acquired. That sounds like a lot, but I'd only need 18.84 fat quarters to make up the difference (or about 4.75 yards of fabric, assuming 45-inch width). And my hexi calculations have never included the irregular stash remnants I'm planning to add for textural variation:
• .81 yards plain yellow cotton
• 1 yard plain gold silk
• .94 yards plain blue silk
• .44 yards plain cream silk
• .59 yards plain brown silk
• 1.75 yards printed mustard cotton
• .5 yards printed light yellow cotton
That's almost exactly 6 yards of fabric.
I might still get just a few more prints...because it wouldn't do to have too many hexis of the same pattern, and I'm not sure I want to eke every possible hexagon out of the silks. They're meant to be textural accents, which implies that they shouldn't occur at the same (or greater) frequency as most of the cotton prints. If I only used half a yard of the mustard print, and assumed no more than .25 yard of each silk, I'd be adding 2.81 yards of fabric to my existing fat quarters, which would leave me about 2 yards short.
(I can stop whenever—shut up, stop laughing—whenever I want.)
Comments
Post a Comment